D'emblée Piaget présente dans ce chapitre une vision complètement renouvelée de l'équilibration qui en 1957 déjà (JP57) était considérée comme le facteur explicatif central de la genèse des structures de la raison pratique, intellectuelle et morale, ainsi que de l'intelligence sensori-motrice et de la construction de la réalité perçue chez le bébé. Il ne s'agit plus, dans cette nouvelle approche, de livrer un modèle statistique et relativement abstrait de l'équilibration largement inspiré des théories et des concepts de la mécanique classique et de la thermodynamique. Le but est maintenant beaucoup plus ambitieux: décrire le plus concrètement possible, en s'inspirant des nombreux faits recueillis dans des recherches idoines, mais sans perdre la généralité théorique, le "mécanisme causal" de l'équilibration et de ses variétés. Retrouvant la richesse de l'approche tout à la fois organique et fonctionnelle autant que structurale qui était celle des travaux sur la naissance de l'intelligence et de la construction du réel chez l'enfant entre 0 et 2 ans (JP36, JP37), Piaget commence par rappeler comment l'intelligence humaine est le fait de schèmes assimilant la réalité extérieure (à laquelle il donne sens) et s'y accommodant; ainsi que de systèmes composés de schèmes exigeant par la force des choses des assimilations et des accommodations réciproques. De ce rappel des recherches des années trente, mais aussi du rappel implicite de l'intuition de départ de toute l'oeuvre de Piaget – le rôle primordial des totalités, de leurs parties, et de la conservation mutuelle qui les rattachent les unes aux autres –, résulte une démultiplication des fonctions et des variétés de l'équilibration. Toutes découlent de l'équilibration la plus fondamentale, celle qui se produit entre l'assimilation et l'accommodation qui sont, aux yeux de Piaget, les processus les plus généraux caractérisant les systèmes vivants, à quelque niveau que ce soit (biologique, psychologique, social). Cette équilibration se décline ensuite entre celle qui implique l'organisme et son milieu, ou, sur les plans psycho-sociologiques et cognitifs, le sujet et l'objet, mais aussi celle qui porte sur les parties (celles, organes, schèmes) dans la mesure où celles-ci en viennent à se coordonner les uns aux autres. Enfin, troisième variété d'équilibration (il en est d'autres), celle qui concerne le tout et ses parties, c'est-à-dire le mouvement de différenciation des dernières et le mouvement contraire d'intégration par lequel le tout cherche à se conserver et, donc, à conserver les parties qui le composent.

La thèse que va soutenir Piaget dans ce chapitre est celle selon laquelle, pour le vivant contrairement aux machines cybernétiques construites par l'homme, la régulation suprême est précisément la totalité organique que compose tout système vivant (thèse qui rejoint ou que rejoint celle de l'autopoïèse chère à H. Maturana et F. Varela). Un constat vient compléter cette thèse. En ce qui concerne la psychogenèse des systèmes cognitifs, l'un des moteurs principaux de l'équilibration est la dissymétrie initiale entre le positif (toute action est initialement positivement orientée, y compris lorsqu'il s'agit pour le jeune enfant de s'opposer à une action extérieure) et le négatif. L'une des caractéristiques les plus révélatrices du travail de l'équilibration au cours de la psychogenése est la construction des négations permettant à l'enfant de dépasser dépasser les nombreuses perturbations ou contradictions dues à ce déséquilibre initial, de combler les lacunes, de compenser progressivement ces perturbations et lacunes, donc dépasser les déséquilibres de départ – un processus qui aboutira finalement, mais cela n'est plus qu'une partie du problème, certes très importante du point de vue de l'explication de la raison, à la construction des structures cognitives durablement équilibrées de la raison opératoire, même si elles sont elles aussi appelées à être dépassées par des structures opératoires toujours plus puissantes créées au niveau toujours plus abstrait (au sens de l'abstraction réfléchissante) des sciences logico-mathématiques. Enfin, et dans le même sens, ce chapitre esquisse une morphologie des régulations qui offre l'intérêt de montrer comment, en effet, les opérations logico-mathématiques découvertes chez l'enfant et chez l'adolescent sont, ainsi que le remarquait le cybernéticien W. R. Ashby, des régulations parfaites au sens où chaque opération possède son inverse ou sa réciproque pour le sujet (dont le système cognitif opératoire concerné) qui la pense et traite les problèmes résoluble au moyen de ce système.

Ce deuxième chapitre confirme la nouvelle approche beaucoup plus concrète – basée sur l'examen de faits explicitement recueillis en vue d'étudier les mécanismes généraux de construction cognitive – que Piaget adopte dans cette étude sur l'équilibration, comparativement à la méthode adoptée dans "Logique et équilibre" (JP57). Ainsi annonce-t-il d'emblée, en première page de ce chapitre, l'utilité d'examiner comment l'équilibration "se déroule concrètement lors des interactions entre le sujet et les objets". Il s'agit de faits recueillis en particulier dans les recherches alors toutes récentes sur "La prise de conscience" et "Réussir et comprendre" (mais, aussi des fines observations recueillies par Inhelder, Sinclair et Bovet dans leur recherche sur "Apprentissage et structures de la connaissances", PUF, 1974). Ces faits sont réexaminés ici en rapport avec les questions (1) d'équilibration des observables sur l'objet et des observables sur l'action propre (= action propre du sujet agissant sur l'objet), (2) d'équilibration des coordinations inférentielles portant sur les actions propres et des coordinations attribuées par le sujet aux objets dans le contexte des explications causales, ou simplement appliquées aux objets réels ou symboliques), et enfin et surtout (3) de l'équilibration sous forme de cycles et de spirale de cette double équilibration des observables d'un côté, et des coordinations de l'autre.

Ce rapport aux faits recueillis pour mieux cerner les prises de conscience, les régulations de l'action, l'abstraction réfléchissante… mais aussi le rôle fécond des conflits cognitifs dans les constructions opératoires (voir opus cité de Inhelder et al. ci-dessus) n'empêche nullement Piaget d'avoir en vue, dans ce chapitre, les principaux résultats de l'épistémologie génétique concernant les mathématiques et les sciences physiques, qui éclairent les nouveaux modèles ici proposés de l'équilibration et de ses variétés, tout autant que ces modèles permettent d'approfondir, de mieux cerner les différences entre la pensée mathématique et la pensée physique.

La deuxième partie de ce chapitre contient une description des étapes des compensations qui permettent au sujet d'annuler les perturbations ou de dépasser les lacunes des systèmes cognitifs précédemment construits. Trois types de conduites sont en particulier distinguées: (1) les conduites alpha, annulant, rejetant ou ignorant l'élément perturbateur d'un système cognitif, (2) les conduites beta, intégrant cet élément et compensant son effet déstabilisateur, et enfin (3) les conduites gama, propres aux systèmes opératoires, qui permettent d'anticiper toutes les variations possibles.

Après la présentation générale de sa nouvelle conception de l'équilibration (majorante) exposée dans les deux premiers chapitres de son maître ouvrage de 1975, Piaget reconsidère dans ce troisième chapitre ses anciennes recherches sur le développement des structures sensori-motrices, perceptives et spatiales dans le but de démontrer dans le détail l'applicabilité du nouveau modèle par rapport aux faits connus. Il s'agit plus particulièrement de montrer dans ce chapitre que, dès le niveau des conduites sensori-motrices et perceptives, les constructions du sujet relèvent bien d'un d'un mécanisme d'équilibration, en d'autres termes que, de manière tout à fait générale, on y trouve à l'œuvre des régulations permettant aux schèmes d'annuler les déséquilibres résultant, par exemple, de leur défaut d'adaptation par rapport aux objets ou aux événements que le sujet cherche à assimiler (regarder, écouter, saisir, déplacer, modifier, etc.)… Notons toutefois que, en ce qui concerne l'application du modèle général exposé dans le deuxième chapitre aux faits observés dans les deux premières étapes de développement de l'intelligence sensori-motrice, ce modèle est adapté par son auteur pour tenir compte d'une caractéristique essentielle des conduites des premiers mois qui suivent la naissance: l'indifférenciation, pour le sujet lui-même, entre ce qui relève du soi (non encore reconnu) et du monde extérieur (en d'autres termes, des observables sur soi et des observables sur l'objet).

Dans ce chapitre, Piaget reconsidère les anciennes études sur la construction des quantités (illustrée ici par le développement de la notion de substance), de la quantification de l'inclusion logique et de la sériation logique en utilisant la nouvelle conception de l'équilibration exposée dans les précédents chapitre.

Voilà dans quels termes Piaget présentent ce chapitre au tout début de celui-ci: "L'équilibration des notions de conservation donne lieu à des problèmes complexes, traités trop sommairement en notre essai de 1957 (Logique et équilibre) comme s'il ne s'agissait que de probabilités de rencontre entre le sujet et les propriétés de l'objet, alors qu'il intervient des régulations compensatrices conduisant en particulier à la mise en correspondance des aspects positifs et négatifs des transformations." Ajoutons que Piaget s'intéresse beaucoup plus qu'il ne le faisait dans le passé aux conduites intellectuelles effectives par lesquelles le sujet peut être amené à résoudre les problèmes cognitifs que lui pose le traitement des quantités… On aperçoit également mieux, à la lumière de l'analyse des quelques exemples illustrant ce chapitre, ce que peut signifier, du point de vue de l'épistémologie génétique, la thèse de l'interaction sujet-objet, ainsi que la dialectique de l'équilibration entre les affirmations et les négations qui est l'une des causes majeures de la progression des connaissances et de la construction des structures opératoires.

Après avoir dans les chapitres précédents exposés son modèle d'équilibration dans lequel sont reliés en étapes successives et par des régulations de différents niveaux les observations sur l'objet et sur le sujet, ainsi que les coordinations relatives aux objets (causalité physique) et les coordinations logico-mathématiques propres au sujet, Piaget procède dans ce dernier chapitre, à une analyse fonctionnelle et psychologique serrée de la construction, par équilibration, des observables puis des coordinations.

Dans une première partie qui concerne les observables, il note que leur construction fait intervenir à la fois le "donné" perceptif et l'assimilation qu'en fait le sujet à travers l'activité de conceptualisation. On y apprend tout d'abord qu'à ses yeux le perceptible peut agir sur le sujet alors même que celui-ci le rejette. Une telle assimilation peut en effet conduire au début de la construction de la construction d'un observable à des conflits ou des contradictions que le sujet va alors chercher à éviter en refoulant ou en réprimant ce qu'à un certain niveau il a pourtant perçu, avant d'en arriver au contraire à dépasser ces conflits en transformant les schèmes d'assimilation cognitive ou de conceptualisation. Une telle analyse fonctionnelle et psychologique de l'activité du sujet dans sa confrontation avec le perceptible n'est pas sans évoquer l'approche freudienne. En un sens, Piaget ne fait ici que développer, en les différenciant à partir des faits recueillis dans les recherches des années 1970, les liens anciennement entrevus entre le fonctionnement de l'intelligence représentative et le fonctionnement de la pensée tel que Freud l'avait interprété dans le contexte de la vie affective de ses patients.

Toujours à propos de l'assimilation des observables, Piaget examine ensuite comment, dans une seconde étape dans laquelle l'enfant ne procède plus par refoulement, l'intervention des régulations compensatrices va aboutir à la constitution de prérelations (par exemple, à propos de la sériation de baguettes de longueurs différentes, par regroupement des différences et des ressemblances en catégories de plus en plus fines: les plus petites, alors rangées ensemble sans tenir compte de leurs différences, les un peu plus grandes, les encore un peu plus grandes, …, enfin les plus grandes) puis de relations entre observables (dans l'exemple de la sériation, la mise en relation de chacune des baguettes, de la plus petite à la plus grande, ou inversément, ce qui implique qu'une baguette peut être à la fois plus grande que la précédente et plus petite que la suivante, la transitivité de la relation asymétrique, etc.).

Dans une troisième étape, Piaget examine la progression des coordinations attribuées aux objets (donc de la causalité) ainsi que la progression des coordinations logico-mathématiques qui concernent le sujet. Là encore, Piaget s'arrête longuement sur le rôle des régulations et de leur caractère compensateur dans cette double progression des coordinations qui, pour les coordinations propres au sujet, aboutit à la construction de structures cognitives stables.

En définitive, en revenant sur le caractère essentiel de compensation propre aux régulations et mis en lumière tant sur le plan de la construction des observables et de leur mise en relation que sur celui des coordinations, Piaget parvient à dégager la raison pour laquelle les régulations propres à l'équilibration des structures cognitives expliquent la forme "finale" de ces structures. C'est que, de par ce caractère, les régulations elles-mêmes comportent une forme mathématique, forment qu'elles impriment d'une certaine manière aux contenus sur lesquelles elles portent. Sur le terrain de la construction logico-mathématique, il y a ainsi homogénéité totale entre l'outil (la régulation et sa forme logico-mathématique) et le produit de l'équilibration. Ou comme l'écrit Piaget, sur le terrain logico-mathématique, la régulation "ne revient qu'à modifier des formes en utilisant ses propres formes" (p. 166). Partout ou la régulation intervient, elle aboutit ainsi à introduire du logico-mathématique, y compris dans la réalité physique telle qu'elle est perçue et connue par le sujet.

Ce constat que dresse ainsi Piaget lui permet de justifier son affirmation déjà ancienne selon laquelle les opérations qui composent les structures opératoires ont leur source et ne sont que l'aboutissement des régulations observées dans les étapes qui précèdent leur apparition chez le sujet. Elles sont bien en ce sens des régulations parfaites, et elles comportent elles aussi ce caractère de compensation propres aux régulations en général (chaque opération voit son effet compensé par une opération inverse, réciproque ou corrélative, ce qui permet au sujet de retrouver tout état de pensée logique préalablement atteint; c'est là la réversibilité opératoire que Piaget a depuis longtemps identifiée comme étant le trait le plus caractéristique de la pensée logique).

Enfin, Piaget termine ce chapitre par une longue conclusion dans laquelle il insiste sur la dimension ouverte de toute construction cognitive, y compris en ce qui concerne les structures opératoires, qui sont sources de nouvelles possibilités de pensée, de nouveaux problèmes imprévisibles qui exigeront le dépassement de ces structures, la construction de nouvelles qui englobent les précédentes, ce qui explique le caractère à la fois novateur et orienté du développement cognitif et de l'histoire des sciences, etc.

Les réponses qu'apportent Piaget dans une première annexe aux objections que ses collègues du CIEG lui ont adressées lui permettent de préciser certaines thèses exposées dans les chapitres de cet ouvrage. Entre autre précision, on y trouvera la définition qu'il donne à la notion de compensation. En réponse à une objection concernant le caractère qui serait exclusivement descriptif de ses travaux sur l'équilibration majorante, Piaget donne les raisons fonctionnelles et structurales qui font, à ses yeux, de cette équilibration et de ses différents mécanismes une explication et même l'explication centrale de la genèse des structures cognitives. Cette réponse est d'autant plus intéressante qu'elle permet de prendre connaissance du "degré de scientificité" de sa conception, tant sur le plan de la description (= les faits, les observables) que de l'explication (= les déductions, les coordinations inférentielles reliant les faits les uns aux autres).

La deuxième annexe relie la notion d'équilibration cognitive aux recherches sur les correspondances, les morphismes et leurs transformations réalisées parallèlement au CIEG. Quant à la troisième annexe, elle révèle la similitude qui existe, selon Piaget, entre le mécanisme de phénocopie par lequel le génome d'une espèce en vient peu à peu à intégrer des adaptations qui se font d'abord sur le plan des adaptations individuelles, et la façon dont, sur le plan cognitif, les régulations se font d'abord par simple rejet ou réaction aux perturbations rencontrées par les schèmes de conduites et de conceptualisation, avant d'être peu à peu intégrées et compensées par des régulations dites beta, puis même d'être anticipées par les systèmes opératoires dans lesquelles chaque opération ou affirmation est mise en rapport, au sein même du système auxquelles elle appartient, avec son inverse ou sa réciproque.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

L'ouvrage dont ce chapitre est extrait est une analyse logique (ou logistique) de l'ensemble des structures d'opérations de transformations (groupes) et de mises en relation (réseaux) possibles des opérations de la logique propositionnelle ternaire (reliant de toutes les manières possibles 3 propositions qui composent le raisonnement logique — dont le raisonnement logique élémentaire dans lequel une proposition sert de moyen terme aux deux autres que sont la prémisse et la conclusion).

Note d'édition:
Vue la complexité de la mise en page et des formules algébriques utilisées dans ce chapitre par Piaget, nous renonçons à l'éditer au moyen d'un logiciel de reconnaissance et nous contentons de le livrer tel quel à nos visiteurs.

Piaget présente dans cette introduction les deux buts principaux de cet ouvrage. Le premier est d'étudier les débuts de la fonction symbolique et de la pensée représentative (y compris le symbolisme « inconscient » des psychanalystes) en cherchant à en dégager les caractéristiques propres, telles qu'elles se manifestent entre la deuxième année et la quatrième après la naissance de l'enfant, c'est-à-dire avant la construction de la pensée opératoire concrète et des "intuitions articulées" qui la préparent entre 4 et 6 ans environ. Le jeu symbolique et l'image sont deux vecteurs importants de cette fonction, d'où le soin que prend l'auteur à en retracer les sources, dans le jeu d'exercice et l'imitation tels qu'ils se développent dans les mois qui la précèdent. Par ce biais, Piaget se donne les moyens d'atteindre le deuxième but de cet ouvrage, à savoir examiner comment cette première forme de "pensée représentative" fait le pont entre l'intelligence sensori-motrice et "les formes opératoires de la pensée".

Bien qu'ayant déjà été étudiée dans les années 1920, la question du langage n'est pas complètement absente de cet ouvrage portant sur une pensée encore essentiellement égocentrique (au sens très particulier où Piaget entend ce terme). Le langage, qui sera certes l'une des conditions d'acquisition de la pensée opératoire, est ici considéré seulement en tant que son usage entre 2 et 4 ans environ révèle des caractéristiques similaires à celles de la fonction symbolique, dont il est d'ailleurs l'une des composantes.

Enfin, relevons que, dès cette introduction, Piaget prend position par rapport aux critiques que lui avait adressées Henri Wallon au sujet de la continuité entre l'intelligence sensori-motrice et la pensée représentative et du rôle du facteur social dans la genèse de cette dernière.

Après une brève introduction à cette première partie ayant pour objet "La genèse de l'imitation", Piaget présente dans ce chapitre les trois premières étapes de cette genèse: (1) la première dans laquelle aucune conduite d'imitation n'a été constatée chez ses trois enfants, (2) la deuxième dans laquelle, vers 1 mois, apparaissent sporadiquement des comportements reproduisant ceux d'autrui, mais seulement à propos de "réactions circulaires primaires" ou de "premiers schèmes réflexes différenciés" auxquels le modèle présenté peut être assimilé et entraîner sa reproduction (l'action de pleurer par exemple, ou la reproduction sporadique de sons que le bébé vient de produire, etc.), (3) la troisième dans laquelle, vers 4 mois, apparaissent des conduites plus systématiques d'imitation de sons appartenant au répertoire de ceux que l'enfant sait produire ou de mouvements que le sujet a déjà lui-même préalablement exécutés "de manière visible pour lui" — en d'autres termes les premières esquisses de conduite intentionnelle d'imitation (mais sans qu'il y ait besoin de construire un nouveau schème générateur du comportement observé et, donc, d'utiliser l'intelligence à cet effet, ce qui sera le cas au stade IV; on pourrait ainsi qualifier de "presque intentionnelle" l'imitation du troisième stade, ceci en reprenant l'expression utilisée par Piaget pour caractériser les réactions circulaires secondaires qui apparaissent au troisième stade de la naissance de l'intelligence).

Sans que Piaget ne nie l'existence de comportements non intentionnels d'imitation susceptibles d'être acquis par des mécanismes tels que le dressage ou l'apprentissage conditionné, ce qui intéresse ici l'auteur est donc essentiellement la genèse de la toute première ébauche de conduite intentionnelle d'imitation, et ce qu'il cherche à montrer dans ce premier chapitre est la façon dont, à ses débuts, cette conduite s'inscrit dans le simple prolongement des caractères circulaire et accommodateur propres aux schèmes d'assimilation sensori-moteurs. En ce sens, la conduite d'imitation est directement liée à la genèse de l'intelligence sensori-motrice, la progression ulltérieure de celle-ci fournissant à l'imitation les instruments permettant au bébé non plus seulement d'imiter les actions d'autrui qu'il sait déjà produire lui-même (ce qu'il fait au stade 3), mais, comme le révéleront les observations des stades 4 à 6 présentées dans les chapitres deux et trois, de coordonner de manière appropriée les schèmes déjà acquis pour produire le comportement imitant une action plus ou moins complexe n'appartenant pas au répertoire de ces schèmes, ou encore pour produire des mouvements invisibles de son visage imitant les mouvements du visage d'autrui. Ce n'est qu'alors que naîtra véritablement la fonction ou la conduite spécialisée d'imitation…

Voilà une image résumant l'essentiel de la structure des premières imitations:
 
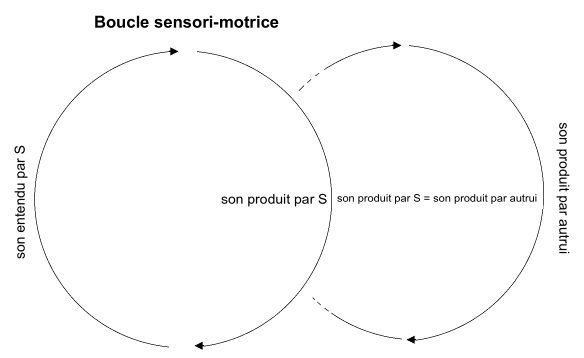
1° Le bébé produit et entend (stade 2) ou sait produire (stade 3) un son; 2° autrui produit le même son; 3° ce dernier est assimilé par le bébé au schème sensori-moteur (à la boucle sensori-motrice) qu'il possède déjà; 4° le schème déjà activé (stade 2) ou susceptible d'être activé (stade 3) l'est à nouveau…

Ce chapitre rapporte les premières formes pleinement intentionnelles d'imitation telles qu'elles se manifestent au quatrième et cinquième stade du développement de l'intelligence sensori-motrice.

Au quatrième stade, l'enfant va utiliser ses capacités d'accommodation intentionnelle des schèmes d'action déjà acquis pour modifier ceux-ci et créer de nouveaux schèmes lui permettant de reproduire par tâtonnement et approximativement de nouvelles actions ou de nouveaux sons produits devant lui par autrui; ou bien encore il va utiliser ses capacités d'assimilation réciproque de ses schèmes, et donc ses capacités inférentielles naissantes, pour repérer par tâtonnement, parmi les mouvements de son propre visage invisibles pour lui mais qu'il sait déjà produire, ceux qui correspondent aux mouvements qu'il voit réalisés par autrui et qu'il cherche activement à reproduire et donc à imiter.

Au cinquième, l'enfant va recourir à sa capacité nouvelle d'inventer, par expérimentation active ou combinaison active des schèmes acquis, de nouvelles conduites productrices de résultats inattendus ou recherchés, pour imiter non plus globalement mais avec précision des mouvements nouveaux réalisés par autrui, y compris des mouvements invisibles du corps propre (se toucher le front avec l'index, par exemple).

Ce chapitre est composé de trois parties: une première dans laquelle Piaget décrit la véritable mutation que connaît l'imitation au sixième stade de développement des conduites sensori-motrices (qui est aussi le stade où apparaît la fonction représentative, ceci grâce en particulier aux progrès de l'intelligence et de l'imitation); une deuxième dans laquelle il décrit à grand trait l'évolution ultérieure de l'imitation et de l'image (celle-ci se rattachant étroitement à celle-là), en ouvrant ainsi la porte aux travaux qu'il consacrera quelque 20 ans tard avec B. Inhelder aux images mentales. Enfin, la troisième partie porte sur une discussion serrée de deux conceptions de l'imitation (l'une de H. Wallon l'autre de P. Guillaume) qui étaient proposées dans les années où Piaget développait sa propre théorie à partir des observations minutieusement recueillies auprès de ses trois enfants.

Le sixième stade du développement de l'intelligence sensori-motrice, et donc aussi de l'imitation, se caractérise par la constitution de la fonction représentative. L'imitation joue un rôle important dans cette constitution. L'imitation pleinement différenciée et intentionnelle des stades 5 et 6 se faisait toujours dans le contexte de la perception du modèle imité. Avec le sixième stade surgit une imitation qui se libère de cette dépendance et qui peut être différée et plus généralement se dérouler en l'absence du modèle imité. Un enfant d'une année et quelques mois voit par exemple un autre enfant réaliser une action que lui-même n'a jamais effectuée. Il peut reproduire cette action non pas immédiatement, mais un ou quelques jours après. Au moment de la perception du modèle, l'imitation reste virtuelle, c'est-à-dire n'est qu'intérieurement esquissée, sans même que l'enfant en ait conscience. C'est après coup, dans des circonstances qui certes peuvent évoquer l'action du modèle, que l'action d'imiter se déploie pleinement. Cette capacité qu'à l'ancienne imitation du stade 5 — comme celle d'ailleurs du stade 4 — de rester (au sixième stade) virtuelle, de ne faire que s'esquisser intérieurement, fournit le matériau de l'image (mentale) à venir. Mais il y a plus:

Dès le sixième stade la capacité qu'à l'enfant de différer l'imitation, s'accompagne de la possibilité, pour le sujet, d'en devenir d'une certaine manière le maître et de la transformer en symbole, c'est-à-dire en représentant d'un autre objet. L'imitation peut n'être plus le motif de l'action en cours (imiter pour imiter); elle peut permettre de se représenter, en les imitant, des mouvements ou des transformations perceptibles ou non des objets, dans le but de les catégoriser (ou de les "classer"), de les comprendre ou de résoudre un problème d'intelligence pratique les concernant. L'exemple protoypique ici est celui de Lucienne qui, voulant sortir une chaîne d'une boîte d'allumettes à peine entre-ouverte, imite avec sa bouche le mouvement d'ouverture et de fermeture de cette boîte (au sixième stade, elle sait imiter en l'absence du modèle). Comme elle sait reconnaître tactilement (avec ses doigts) le mouvement de sa bouche (qu'elle connaît par ailleurs par assimilation avec les mouvements de la bouche d'autrui, résultat d'anciennes imitations — quatrième et cinquième stades — des mouvements invisibles du corps propre), elle n'a plus qu'à transférer sur la boîte d'allumettes le mouvement de son index qui accompagne parfois l'ouverture et la fermeture de sa propre bouche, ou de celle d'autrui. Le mouvement de sa bouche, cette imitation en l'absence du modèle, représente pour elle le mouvement visé (et souhaité) de la boîte d'allumettes. Il est à la fois le représentant du mouvement visé, son image donc, et le moyen par lequel sera reconnue la solution au problème auquel Lucienne se heurte… Un pas devra encore être franchi pour que le sujet en vienne à utiliser intentionnellement, comme représentant de réalités non présentes, les esquisse intériorisées des schèmes d'action, et pour que soient constituées par ce sujet et pour ce sujet de véritables images mentales. C'est ce parcours — caractérisé par l'explosion de la fonction symbolique — que Piaget décrit dans la troisième partie de ce chapitre III.

Pour Piaget, la fonction symbolique ne surgit pas ex nihilo. Elle naît de la combinaison, rendue possible à une certaine étape de leur développement, des fonctions assimilatrices et accommodatrices des schèmes, et de leurs produits (imitations externes et internes, mais aussi significations qui leur sont attribuées). On voit ici, comme dans d'autres contextes, que ce qui fait toute la difficulté de cette partie de l'œuvre de Piaget est que celui-ci s'efforce de répondre à la plus ambitieuse des questions psychologiques: connaître et expliquer l'origine et la genèse des fonctions intellectuelles.

Dans ce chapitre, Piaget montre comment, pendant les 6 stades de développement des conduites sensori-motrices (qui, au sixième stade voit apparaître les débuts de la représentation), la genèse du jeu se déroule en parfaite synchronie avec celles de l'intelligence et de l'imitation. Il met également en évidence le paradoxe apparent que constitue le jeu symbolique (la conduite du "faire semblant") qui apparaît au sixième stade. Dans les stades précédents, l'imitation (primat de l'accommodation) était toujours antithétique avec le jeu (primat de l'assimilation). Au sixième stade au contraire, le jeu utilise la caractéristique majeure de l'imitation de ce stade, à savoir la capacité d'évoquer un objet absent ou un événement non actuel (ceci de la même façon que l'intelligence du sixième stade peut recourir à l'imitation représentative pour atteindre un certain but). Ces trois caractéristiques: le synchronisme de développement, l'opposition initiale, puis la capacité finale de se combiner dans une même conduite telle que le jeu symbolique s'expliquent par le lien qu'ont le jeu, l'imitation et l'intelligence avec les deux fonctions de base de tout schème d'action que sont l'assimilation, l'accommodation, ainsi qu'avec leur séparation et leur spécialisation progressive rendant finalement possible leur combinaisons différenciée au sein d'une même action.

Voilà dans quels termes Piaget conçoit la façon dont l'antithèse initiale est finalement dépassée en raison des progrès de ces deux fonctions de base, et plus particulièrement de l'imitation, rendant possible leur coopération: «En conclusion, tant qu'il s'agit d'intelligence, d'imitation et de conduites ludiques toutes trois exclusivement sensori-motrice, l'imitation prolonge l'accommodation, le jeu prolonge l'assimilation et l'intelligence les réunit sans interférences compliquant cette situation simple. Avec les conduites différées et intériorisées à la fois qui marquent les débuts de la représentation, l'imitation, qui développe alors une accommodation aux objets absents et pas seulement présents, acquiert par le fait même une fonction formatrice de « signifiants » par rapport aux significations (aux « signifiés ») adaptées ou ludiques selon qu'elles émanent de l'assimilation accommodée actuellement ou de l'assimilation déformante, caractéristiques de l'intelligence ou du jeu» (p. 110).

Dans les années 1920 et 1930, conformément à une démarche qui lui était coutumière, Piaget — seul ou avec l'aide de sa femme et de ses collaborateurs de l'Institut Jean-Jacques Rousseau (à Genève) — a recueilli un très grand nombre d'observations de comportements ludiques, aussi bien chez ses trois enfants, que chez des enfants fréquentant la "Maison des Petits" rattachée à cet Institut, ou encore jouant dans la rue. En bon naturaliste, il n'a dès lors pas manqué d'établir une classification apte à couvrir l'ensemble des comportements qui, des jeux d'exercices (seuls observés dans la première année post-natale), aux jeux de règles (à partir de 4-5 ans) en passant par les jeux symboliques (dominant entre 2 et 6 ans environ), pouvaient être assimilés à des jeux. Ce faisant, Piaget n'a pas manqué de discuter les principales classifications qui étaient alors proposées par des auteurs tels que K. Groos et C. Bühler. Ce sont cette discussion et sa propre classification que le lecteur pourra découvrir dans ce chapitre qui, à la différence du précédent, va au-delà des faits décrits dans le chapitre IV, qui s'arrêtait à la fin de la période sensori-motrice et au tout début de la pensée symbolique. Les jeux de règles ayant déjà été exposés en 1932 dans l'ouvrage sur "Le jugement moral chez l'enfant" (JP32), et les premiers jeux d'exercice ayant déjà été examinés et ordonnés de manière détaillée dans le chapitre IV, c'est essentiellement à l'examen et l'exposé de l'évolution des jeux d'exercice et des jeux symboliques "à partir de l'apparition du langage" que se consacre plus spécialement ce cinquième chapitre, l'explication couvrant l'ensemble des jeux d'exercice, symboliques et de règles étant réservée au chapitre VI.

Notons enfin que le travail de classification auquel procède Piaget rejoint celui réalisé sur le terrain de la malacologie ou, ultérieurement, de la botanique (JP66_13), par l'attention portée aux différences de structure que présentent les jeux d'exercice et les jeux symboliques au cours des étapes que chacun de ces deux types de jeux traverse.

Pour Piaget, à l'opposé des activités visant l'imitation laborieuse du réel ou des actions d'autrui, lors desquelles le pôle accommodateur de la conduite l'emporte sur le pôle assimilateur inhérent à toute conduite, le jeu s'explique de manière tout à fait générale par le primat de l'assimilation sur l'accommodation. Se pose alors le problème des jeux symboliques, qui font appel à des symboles imitant dans une certaine mesure les réalités simulées dans ces jeux (par exemple, l'enfant qui joue à se coiffer avec un bâton, ou l'enfant qui joue à être autrui). Mais ces jeux ne dérogent pas à la thèse du primat de l'assimilation sur l'accommodation dans la mesure où le but que poursuit alors le sujet n'est pas d'imiter le réel, mais de prendre plaisir à le simuler, à le reproduire, à faire ceci ou cela, ou à être ceci ou cela, sans se soucier des contraintes effectives qu'imposerait une fidèle et laborieuse imitation ou reproduction de ce réel. En d'autres termes, dans les jeux symboliques, l'activité accommodatrice est asservie à la libre activité d'un sujet qui ne cherche ni à suivre de près les contours du réel, ni à connaître celui-ci (un tel objectif de connaissance se caractérisant par la recherche d'un équilibre entre les deux pôles assimilateurs et accommodateurs de toute conduite), mais avant tout à se faire plaisir. C'est pourquoi dans le jeu symbolique, les symboles utilisés peuvent n'avoir qu'une similitude très vague avec les objets réels dont ils sont le substitut, comme ce peut être d'ailleurs le cas aussi, mais pour une toute autre raison, lors d'une activité proprement cognitive s'appuyant sur des symboles imagés.

Piaget conclut ce chapitre par un dernier paragraphe consacré cette fois au jeu de règles, dont il avait examiné la genèse chez les enfants dans son étude sur Le jugement moral chez l'enfant (JP32). Le principe de ce jeu reste l'assimilation (ludique) du réel au moi, mais avec conciliation de "cette assimilation avec les exigences de la réciprocité sociale".

Le jeu symbolique est l’un des trois grands types de jeux dont Piaget a retracé la genèse, soit dans le présent ouvrage, soit dans JP32 (ouvrage dont le premier chapitre portent sur la genèse des jeux de règles, qui succèdent dans leur structure aux jeux d’exercice puis au jeux symboliques, seuls présentés de manière relativement exhaustive dans JP45, chapitres IV, V et VI). Comme tout jeu impliquant le réel, il repose sur le primat de l’assimilation sur l’accommodation ; mais il se différencie toutefois par l’usage tout personnel (ou «égocentrique» au sens piagétien) de substituts du réel ou symboles offrant, pour leur utilisateur, une similarité plus ou moins grande avec ce qu’ils représentent. Point central de la théorie piagétienne, les significations que l’individu attribue à ces symboles proviennent non pas de ce rapport de similarité, mais de leur assimilation aux schèmes alors activés. Toutefois, en très bon connaisseur de la psychanalyse et de ses variantes (Freud, Jung, Klein, Silberer, etc.), Piaget admet que, en certains cas, en plus de la signification manifeste ou «primaire» des symboles ludiques, leur usage peut impliquer une signification dont le jeune enfant ne peut prendre conscience et qui, en ce sens, se rapproche des faits révélés par la psychanalyse lors de son examen des rêves et de leur signification. Piaget parle de «symbolisme secondaire» pour désigner cette sous-classe de jeux symboliques dont il présente quelques exemples. La question se pose alors de savoir si les processus en jeu dans le symbolisme secondaire s'inscrivent ou non en continuité avec ceux présents dans le symbolisme primaire, ou si, au contraire, le symbolisme secondaire serait la source du symbolisme en général, comme tendrait à l'impliquer la théorie freudienne. Tout en reconnaissant la réalité du refoulement, qui peut s’expliquer par les conflits entre schèmes (par exemple entre un désir et un schème de nature normative, ou entre un schème conceptuel et un schème perceptif), Piaget juge superflu d’attribuer à la vie mentale un mécanisme tel que la censure, laquelle, au moyen du symbolisme (dont elle serait alors la source), déguiserait le contenu du rêve pour le rendre acceptable à la conscience (un mécanisme qui impliquerait d'attribuer à l’inconscient ou à une deuxième conscience un pouvoir de tri qui n’apparaît qu’ultérieurement dans le développement intellectuel du sujet conscient). Ce que suggère plutôt l’examen de la genèse du jeu symbolique, c’est au contraire une certaine continuité entre le symbolisme primaire et le symbolisme secondaire, celui-ci n’étant que la conséquence d’une plus grande difficulté de prendre conscience du lien existant entre le symbole utilisé et la réalité dont il est le substitut (en d’autres termes, le jeune enfant ne possède pas le cadre conceptuel qui lui permettrait d’expliciter ce rapport, un état de fait qui peut d’ailleurs se retrouver à des étages supérieurs de fonctionnement de la pensée, comme l’établiront les travaux de la fin des années 1960 ou du début des années 1970 exposés dans JP74a et JP74c). De même, dans les rêves de sujets même adultes, certains symboles ont une signification immédiate ; d’autres une significations plus difficiles à expliciter ; mais cette plus grande difficulté tient encore une fois, pour Piaget, simplement au fait que les schèmes activés dans le rêve relèvent de cette forme de pensée symbolique découverte dans les jeux symboliques des enfants, à partir d’une année et demi ou deux ans, et non pas d’une pensée devenue sociale et rationnelle. Si l’on ajoute le fait que, dans le rêve, la forme d’égocentrisme ou d’autoïsme de la pensée symbolique tend à rejoindre l’adualisme observé chez le nourrisson dans les semaines qui suivent la naissance — un adualisme dont on sait aujourd’hui que, dans sa forme primitive chez le nouveau-né, il n’implique pas l’absence d’échanges éthologiques avec le monde qui l’entoure, mais qui n’en signifie pas moins une absence complète ou presque de la conscience du soi assimilateur — on comprend que Piaget juge inutile l’attribution à l’inconscient de mécanismes spécifiques permettant de tromper le sujet endormi, et relevant donc de la ruse.

Que l’on soit ou non d’accord avec la façon dont Piaget tire ici profit de ses recherches sur la pensée du jeune enfant et plus généralement de l’intelligence humaine pour rendre compte du refoulement freudien et de ses conséquences, ou au contraire pour réduire le mécanisme freudien de la censure aux caractéristiques d’une pensée «autoïste» telle que découverte chez l’enfant de 2-4 ans, la lecture de ce chapitre révèle, comme tous les autres écrits dans lesquels Piaget prend à partie la psychanalyse, les rapports tout à la fois critiques et amicaux que le chercheur et théoricien genevois a entretenus tout au long de son œuvre avec cette discipline (il reconnaît les faits découverts par la psychanalyse, mais en propose une réinterprétation en accord avec les concepts théoriques d'une psychologie renouvelée par les recherches psychogénétiques). Le lecteur pourra aussi y reconnaître, ou y découvrir, à propos de notions aussi obscures que celles de censure et de déguisement, lorsqu’elles sont attribuées aux processus du rêve, ou encore de l'explication que la censure donnerait de l'origine de la fonction symbolique, cette façon constante qu’a Piaget de traquer dans la psychanalyse ce qu’il considère être une erreur de méthode, à savoir prêter sans aucune hésitation aux processus primaires de la pensée des compétences intellectuelles qui n’apparaîtront qu’ultérieurement dans la genèse de la pensée.

Ce huitième chapitre ouvre la troisième et dernière partie de l'ouvrage. Il est précédé de deux pages dans lesquelles est présenté l'objectif central de cette dernière partie sur "La représentation cognitive", à savoir la détermination des relations entre l'image (imitative), le symbolisme ludique et la représentation cognitive propre à l'intelligence représentative.

Piaget examine dans ce huitième chapitre la transformation du schème sensori-moteur en "schème conceptuel", transformation conditionnée par les progrès conjoints de la fonction sémiotique, des schèmes verbaux et donc de la socialisation, mais également de l'intelligence représentative. Il y examine de manière très fine la progression du langage et de ses usages d'abord essentiellement pratiques (lié à l'action et au désir du sujet), puis représentatifs, descriptifs et enfin préconceptuels, depuis l'âge de 18 mois environ, jusque vers 4 ans (sans omettre la dimension communicationnelle et sociale).

Dans cet usage du langage comme outil de conceptualisation, il n'y a pas encore de concept à proprement parler, dans la mesure où l'enfant n'a pas encore construit les opérations et la notion de classe logique. De même, faute de co-ordination opératoire des points de vue, il ne peut livrer (à soi-même ou à autrui) des descriptions d'objets ou de situations autres que celles assimilées ou assimilables à son point de vue. De 2 à 4 ans environ, en raison de l'absence de décentration, les préconcepts partagent avec la pensée symbolique l'absence de généralité, et il en va de même pour les premiers raisonnements. Entre 4 et 6-7 ans apparaît toutefois un "infléchissement" de l'usage des préconcepts "dans la direction du concept opératoire" de par l'apparition d'un début d'emboîtement hiérarchique de ce qui deviendra par la suite des classes logiques.

On voit donc que, dans ce chapitre, ce qui intéresse avant tout Piaget, ce sont, non pas les progrès langagiers en tant que tels, mais leur relation au progrès de l'intelligence logique du jeune enfant. En l'absence de réversibilité opératoire, les signifiants langagiers utilisés pour décrire et concevoir les choses partagent le caractère individuel, le défaut de généralité interindividuelle, des symboles ludiques et de l'usage des images comme autres instruments de représentation du réel.

Piaget, dans ce chapitre de conclusion, parvient en 23 pages à développer une conception du développement des activités sensori-motrice et de la pensée de l'enfant à la fois très riche en extension (par les nombreuses conduites qu'elle vise et qui en constituent le support empirique) et en compréhension (par la portée à la fois différenciatrice et intégratrice des concepts utilisés, dont ceux de schème, d'assimilation et d'accommodation, du primat de l'une ou de l'autre de ses deux fonctions, ou au contraire de leur équilibre plus ou moins stable).

Accompagnée d'un schéma d'ensemble qui la résume parfaitement, cette conception rend compte de la genèse des trois classes de conduites pouvant être rapportées aux deux fonctions de base de la vie psychologique que sont l'assimilation et l'accommodation, ainsi qu'aux rapports d'équilibre ou de déséquilibre que celles-ci entretiennent: (1) l'imitation (sensori-motrice puis représentative, qui culmine dans l'image mentale) et l'imitation réfléchie, (2) le jeu (sensori-moteur puis symbolique avant de devenir jeu de construction et jeu de règles), enfin (3) l'intelligence (sensori-motrice puis représentative préconceptuelle et intuitive, avant de devenir opératoire), sans ignorer le rôle que joue le langage, et donc les interactions sociales, dans l'essor de l'intelligence représentative.

Pour ne pas se méprendre sur la portée très concrète d'une théorie apparemment très abstraite, le lecteur ne doit pas oublier que derrière chaque affirmation théorique livrée dans cette conclusion, se cachent un nombre souvent très grand de ces conduites et schèmes de comportement, que l'auteur a systématiquement observés ou provoqués chez ces propres enfants (entre 0 et 3-4 ans), complétés par des observations recueillies auprès d'autres enfants, dont ceux de la Maison des Petits (l'école associée pendant des années à l'Institut Jean-Jacques Rousseau, institution qui bien plus tard deviendra faculté de psychologie et des sciences de l'éducation de l'université de Genève). En plus de fournir une vision très riche de la vie psychologique du jeune enfant, la lecture attentive de ces observations et des analyses de conduite qui les accompagnent apparaît dès lors comme une condition de pleine compréhension des notions et de la conception théoriques qui composent cette conclusion.

[Texte de présentation; version du 30 mai 2010.]

Composée de trois chapitres, la troisième partie de l'ouvrage sur "La genèse de l'idée de hasard chez l'enfant" porte sur la genèse des opérations combinatoires sous-jacentes au calcul des probabilités et donc à la maîtrise du hasard. Le chapitre 7 porte sur les opérations dites de combinaison, qui, aux côtés des opérations de permutation et des opérations d'arrangement composent l'ensemble des opérations combinatoires. Il faut attendre le stade de la pensée formelle, en tant que caractérisé par la capacité d'opérer sur des opérations, pour que soit maîtrisés ces trois systèmes combinatoires. Au niveau des opérations concrètes, c'est-à-dire entre 7 et 10 ans environ, c'est seulement par tâtonnement que le sujet parvient à trouver les combinaisons possibles d'un certain nombre d'éléments, sans d'ailleurs être assuré de toutes les lister.

[Texte de présentation; version 10 juin 2010]

Composée de trois chapitres, la troisième partie de l'ouvrage sur "La genèse de l'idée de hasard chez l'enfant" porte sur la genèse des opérations combinatoires sous-jacentes au calcul des probabilités et donc à la maîtrise du hasard. Le chapitre 8 porte sur les opérations de permutation, qui, aux côtés des opérations de combinaison (1 à 1, 2 à 2, 3 à 3, etc.) et des opérations d'arrangement (combinaisons n à n tenant compte de l'ordre de placement des éléments et donc des permutations possibles au sein d'une combinaison) composent l'ensemble des opérations combinatoires. Alors que les opérations de combinaison sont maîtrisées au début de la pensée formelle, il faut attendre l'achèvement du stade de la pensée formelle pour que soit pleinement acquis le système, plus compliqué, des permutations. Cet achèvement plus tardif permet de suivre plus en détail l'acquisition progressive de ce système.

[Texte de présentation; version 26 juin 2010]

Composée de trois chapitres, la troisième partie de l'ouvrage sur "La genèse de l'idée de hasard chez l'enfant" porte sur la genèse des opérations combinatoires sous-jacentes au calcul des probabilités et donc à la maîtrise du hasard. Alors que le chapitre 7 portait sur les opérations de combinaisons (1 à 1, 2 à 2, 3 à 3, …, n à n) de n objets ou éléments, et le chapitre 8 sur les opérations de permutations au sein d’un ensemble de n éléments, le chapitre 9 porte sur les opérations d’arrangements, c’est-à-dire de combinaisons n à n tenant compte de l'ordre de placement des éléments et donc des permutations possibles au sein d'une combinaison.

La dernière section de ce chapitre porte sur la "quantification des probabilités fondées sur les arrangements", quantification dont l'exemple le plus célèbre en histoire des sciences réside dans la découverte par Mendel de la loi de reproduction des caractères lors de l'hybridation de variétés héréditaires de petits pois.

[Texte de présentation (version 6 mai 2010).]

Ce chapitre montre comment le procédé de correspondance terme à terme ou binunivoque entre les éléments de deux collections tend à l'emporter progressivement sur le procédé de comparaison de quantités discrètes basé sur la lecture perceptive de l'espace occupé par les éléments des deux collections lorsqu'il s'agit de juger de la conservation ou non de de ces quantités après modification de forme des collections.

Il décrit les trois grandes stades (1. jugement de non-conservation des quantités numériques, 2. oscillation du jugement, 3. jugement de conservation des quantités numériques) par lesquels passe l'enfant pour acquérir une notion de nombre indépendante des caractéristiques spatiales des collections considérées.

Cette introduction générale aux trois volumes d'"introduction à l'épistémologie génétique" peut être décomposée en quatre parties. Dans la première, Piaget présente cette nouvelle discipline qu’il propose à la communauté scientifique et qui est fondée sur l’adoption de méthodes proprement scientifiques; dans la seconde, il expose les grandes solutions classiquement apportées au problème de la connaissance; dans la troisième, il discute un des problèmes centraux de l’épistémologie: le passage, s’il existe, entre le devenir génétique et l’atemporalité des normes logiques; enfin, dans la quatrième partie, il développe quelques réflexions fondamentales quant au cercle sujet-objet propre à tout accroissement des connaissances, et son prolongement, le cercle des sciences. Ajoutons que sont aussi présentées et discutées dans cette introduction l’œuvre épistémologique du mathématicien et philosophe italien F. Enriques, dans la mesure où cette œuvre permet de préciser la spécificité de l’épistémologie génétique, qu’elle anticipait pourtant à bien des égards. Si F. Enriques n’a pas pu aboutir à une solution génétique convaincante, la raison en est qu’il a construit son épistémologie à partir de l’ancienne psychologie associationniste, et non pas de cette psychologie de l’action à laquelle se ralliera Piaget dès ses premiers travaux.

(I) En ce qui concerne la première partie, Piaget présente une nouvelle fois le projet d’une épistémologie scientifique susceptible de conduire à l’accord des esprits sur des problèmes relevant classiquement de la philosophie, mais délimités de manière à pouvoir rendre possible l’application de méthodes scientifiques conditionnant un tel accord. Ce faisant, elle ne fera que suivre le procédé utilisé par les sciences de la nature lorsque elles se sont détachées de la philosophie. Si le tour est venu à l’épistémologie d’accomplir cette démarche, celle-ci est accélérée par le fait que, de manière trop générale, la philosophie universitaire a laissé se creuser un fossé entre elle-même et les sciences. Piaget observe que ce pas a d’ailleurs été esquissé avant lui, notamment par des historiens des sciences ou par des savants intéressés par les questions épistémologiques.

En proposant dans son introduction cette épistémologie génétique dont il a jeté les bases dès les années 1920, Piaget ne fait que conduire à son terme son détachement. Il le fait en premier lieu en lui attribuant comme objectif particulier, non plus de donner d’emblée une réponse à la grande question du rapport de la connaissance (considérée dans sa totalité) à la réalité, mais de chercher à connaître comment se fait l’accroissement de connaissances particulières, propres à chacune des sciences existantes (la logique, les mathématiques, etc.).

En deuxième lieu, vient l’examen des méthodes à adopter pour pouvoir tendre à l’accord des esprits sur les réponses à apporter aux questions particulières soulevées quant à l’accroissement des connaissances dans les sciences logiques, mathématiques, physiques, etc. Piaget suggère de s’inspirer des démarches adoptées par la biologie de l’évolution, ce qui est à ses yeux tout à fait naturel, puisque l’activité cognitive des êtres vivants est le prolongement des processus par lesquels les espèces ou les êtres vivants se sont progressivement adaptés à leur milieu.

Pour connaître les filiations entre les espèces, la biologie a donné naissance aux deux grands sous-domaines de l’anatomie comparée et de l’embryologie (qui toutes deux étudient les structures du vivant. La première porte sur les formes adultes. Certaines filiations entre espèces peuvent être établies par ce biais. Mais cette méthode ne peut atteindre les rapports de filiation les plus anciens. L’embryologie fournit ici un appoint essentiel en conduisant à la mise en évidence de ces liens restés cachés. Or, il en va en partie de même en ce qui concerne cette nouvelle science qu’est l’épistémologie. Hormis la démarche de formalisation qui permet de répondre à des questions de fondements logiques, l’épistémologie a fait un large usage de la méthode historico-critique. Cette méthode permet d’étudier le problème de l’accroissement des connaissances dans une foule de chapitres particuliers de l’histoire des sciences et d’apporter ainsi de nombreux faits susceptibles d’apporter des éléments de réponses aux questions de l’épistémologiste. Il y a cependant une limite: il n’est pas possible de remonter aux sources les plus anciennes des sciences, sources qui se trouvent dans les étapes préscientifiques de l’histoire de l’humanité. Mais de même que l’embryologie permet d’une certaine façon de remonter plus haut que l’anatomie comparée portant sur les formes abouties des espèces, de même une nouvelle discipline, la psychologie génétique, offre une issue à l’épistémologiste soucieux de remonter à ces sources. L’étude du développement des notions physiques, logico-mathématiques chez l’enfant permet d’atteindre en effet des structures de pensée et les notions qui leur sont liées dont on peut supposer qu’elles sont au moins partiellement similaires à celles qui pouvaient se trouver chez les anciens humains. Bien sûr, les enfants d’aujourd’hui sont nourris par la pensée adulte qui les entourent (cette dimension là de l’accroissement des connaissances chez l’enfance relève de ce que Piaget appelle alors la méthode sociologico-critique, méthode qui complète l’étude historico-critique de la progression des connaissances). Mais il n’empêche que pour assimiler ce qui leur est ainsi transmis, ils passent par des étapes qui ne sont pas le reflet des enseignements reçus, mais qui illustrent des formes de pensée et des étapes de développement des notions qui ont précédé les formes de la pensée adulte et de la science actuelle.

(II) La deuxième partie consiste en la présentation de six types de solution possible au problème central de l’accroissement des connaissances — six types qui se distribuent en un tableau à double entrée, selon que (1) les solutions proposées sont ou ne sont pas génétiques (la recherche pourrait mettre en évidence un accroissement fictif en ce qui concerne les connaissances les plus fondamentales, en corroborant par exemple une solution de type platonicienne), et selon que (2) ces solutions attribuent l’essentiel de l’origine des connaissances examinées soit au sujet, soit à l’objet, soit enfin à la relation indissociable que constitue le couple sujet-objet (toute activité cognitive porte sur des objets, mais inversement, toute saisie d’un objet quel qu’il soit implique un cadre d’assimilation inhérent au sujet). Bien que la solution qui sera finalement retenue par Piaget soit génétique et interactionniste (donc basée sur le caractère indissociable du couple sujet-objet, et plus précisément sur le cercle sujet-objet qui sera exposé dans la troisième section de l’introduction), l’auteur montre que chacune des six solutions épistémologiques pourrait se voir confirmée par les méthodes psychogénétique et historico-critique de l’épistémologie génétique. Notons au passage que ce tableau des solutions possibles sera repris et complété par Piaget dans son chapitre final de l’ouvrage collectif Logique et connaissances scientifiques publié en 1967).

(III) La troisième partie expose et discute le problème central auquel se heurte les trois familles de solutions génétiques (l’empirisme, le conventionnalisme, le relativisme): le problème du rapport entre une genèse qui procède dans le temps et des normes proprement intemporelles. Toutes trois font l’hypothèse que les formes et normes logiques ne sont pas données dès le départ, serait-ce virtuellement. Mais l’épistémologie génétique se fait plus précise: elle renverse les relations de prééminence classiquement conçues entre le réel et le possible, ainsi qu’entre l’action et la pensée. Au début de la psychogenèse, le réel peut primer sur le possible et l’action constituer le socle à partir duquel s’édifie la pensée; or, si les faits livrés par l’enquête psychogénétique corroborent cette solution, ils permettraient du même coup de rendre moins énigmatique ce passage du "devenir mental" à la "permanence normative".

(IV) Piaget se penche ensuite sur la question du cercle sujet-objet et de son prolongement que constitue le cercle ou la spirale des sciences, avec ces deux mouvements complémentaires que sont la mathématisation du réel, et, dans le sens inverse, la recherche d’une explication naturelle de l’origine des mathématiques. Il achève alors son introduction en examinant, en rapport avec cette question, le problème méthodologique posé par le rapport entre l’épistémologie génétique et les sciences contemporaines — sciences qui fournissent à celle-ci le référentiel, (c’est-à-dire les connaissances actuelles et la conception que l’on se fait aujourd’hui du réel) au moyen duquel elle étudie les étapes dont elles sont issues! Cette épistémologie ne saurait en effet ni juger que ces connaissances ne puissent à leur tour être dépassées dans le futur, ni considérer que la question des frontières entre le sujet et l’objet soit définitivement tranchée, puisque ce que l’on désigne aujourd’hui comme réalité peut changer en fonction du progrès des sciences. Tout au plus les solutions partielles auxquelles est parvenue l’épistémologie génétique à travers son analyse des différences sciences actuelles et de leurs étapes passées peuvent-elles révéler une orientation générale de la marche des sciences, ou une sorte de «loi générale d’évolution», illustrée dans le cas de la question du cercle sujet-objet et de son prolongement dans le cercle des sciences par les deux mouvements contraires et complémentaires de réduction des mathématiques au réel et de mathématisation de la nature, qui tous deux infirment respectivement l’idéalisme absolu et le matérialisme absolu. Précédemment, Piaget avait d’ailleurs mentionné une autre orientation générale des sciences susceptible d’être tirée des études d’épistémologie restreinte relatives aux différents domaines et sous-domaines des sciences, à savoir le passage d’un état de moindre connaissance vers un état de connaissance plus avancé, passage pouvant être expliqué par un processus général d’équilibration, dont on peut supposer, sans trop céder à la spéculation, qu’il continuera de fonctionner dans le futur. Ainsi ce que Piaget appelle l’épistémologie génétique restreinte (basée sur des recherches particulières) pourrait-elle permettre de rejoindre en partie, mais en partie seulement, les grandes interrogations posées classiquement en philosophie de la connaissance, en apportant des réponses plus scientifiquement fondées.

[version 10 déc. 2009]

Après avoir brièvement décrit en avant-propos les rapports des mathématiques à la réalité physique et les problèmes épistémologiques majeurs soulevés par ces rapports, Piaget se penche sur la question de l'origine et de la signification épistémologiques du nombre.

En ce qui concerne les nombres entiers, Piaget montre comment les résultats des recherches psychogénétiques et des esquisses de modélisations logistiques qui s'y rattachent peuvent contribuer à progresser dans l'ancien débat qui opposait les tenants (dont Bertrand Russell) d'une complète réduction des nombres aux entités plus élémentaires de la logique (la classe logique pour le cardinal d'un nombre, l'ordre asymétrique logique pour le nombre ordinal) aux tenants (dont Poincaré) d'une intuition numérique irréductible aux être logiques. Des résultats de ces recherches Piaget conclut que, si le nombre n'est en effet pas entièrement réductible aux notions logiques de classe et de relation asymétrique logiques, le parallélisme de développement entre classe, relation et nombre suggère que la construction de ce dernier s'appuie en partie sur la construction des deux premières, ce qui conforte la position de Brunschvicg qui, à partir d'une analyse épistémologique serrée de la notion de nombre naturel, concluait à l'impossibilité de concevoir un nombre indépendamment de la prise en considération de la double dimension d'inclusion et de sériation qu'il renferme implicitement.

Pour Piaget d'ailleurs, si réduction il y a entre, d'un côté, le nombre et, de l'autre, la classe et la relation logiques, cette réduction n'est pas à sens unique. Certes le nombre peut être conçu comme produit d'une fusion des opérations de classification et de sériation logiques (des premières, le nombre emprunte le rôle qu'y joue la similitude ou l'équivalence réunissant sans distinction les éléments-unités dénombrés, et des secondes, l'ordre sériel établi entre ces éléments, ordre qui seul permet de les distinguer les uns des autres). Mais ces mêmes opérations de classification et de sériation peuvent tout aussi bien être conçues comme résultant d'une "dissociation" des activités d'emboîtement et de sériation intervenant dans la construction de la suite des nombres et dans l'usage du dénombrement et des opérations arithmétiques. Les groupements logiques sont certes formellement plus pauvres que le groupe des entiers numériques, ce qui tend à suggérer une antériorité (trompeuse) du logique sur l'arithmétique. Aussi la solution tracée par Piaget dans ces pages devrait-elle être nuancée de manière à inclure un résultat psychogénétique dont l'évidence s'imposera de plus en plus par la suite: la maîtrise, par l'enfant, de la quantification logique accompagnant la construction de l'inclusion logique est ou peut être plus tardive que la maîtrise de la quantification arithmétique. Ainsi un enfant de 6-7 ans peut-il porter un jugement de conservation du nombre, indice d'une déjà pleine maîtrise opératoire des premiers nombres entiers et des opérations qui les rattachent les uns aux autres, alors même que, pour lui, la question de savoir s'il y a plus d'éléments dans un sous-ensemble logique que dans l'ensemble logique dans laquelle celui-là est (visiblement ou non) inclus n'a pas ou peut ne pas avoir de sens. (Pour se faire une idée de la complexité que cette question de quantité logique peut poser aux jeunes enfants, on peut se référer au cas de la jeune Anouk, qui avait été interrogée dans le cadre des recherches longitudinales entreprises par Bärbel Inhelder et ses collaborateurs sur le développement de la pensée de l'enfant et de l'adolescent: Anouchka et l’inclusion des fleurs).

Si elle est avérée, cette antériorité de la quantification numérique élémentaire par rapport à la quantification logique implique que l'activité de réunion et d'emboîtement logiques propre à toute classification est plus simple à réaliser lorsque les propriétés distinctives qui permettent d'identifier ou de particulariser les éléments des classes emboîtées les unes dans les autres ne sont pas abstraites de la réalité empirique (comme c'est le cas pour être une tulipe, être une fleur, etc.), mais sont introduites par l'enfant de 6-7 ans qui ordonne les éléments en les dénombrant. Mais quoi qu'il en soit des nuances qu'il convient à apporter à certaines affirmations dans lesquelles Piaget semble accorder — pour des raisons qui tiennent plus de la modélisation logistique que de l'analyse psychogénétique — une sorte de primauté aux opérations logiques de classification et de sériation par rapport aux opérations arithmétiques issues de leur fusion, la thèse d'une intervention concomitante des activités (certes non nécessairement explicitée) de classification et de sériation dans la constitution du nombre opératoire reste valide, comme reste valide l'affirmation selon laquelle le nombre une fois construit contient bien des opérations qui, dans le cadre de l'activité de dénombrement, relèvent tout à la fois de l'inclusion et de la sériation, et donc de la logique des classes et de la logique des relations. Dans la suite de ce chapitre sur la pensée arithmétique, Piaget va d'ailleurs conforter cette thèse en examinant la genèse de l'axiomatisation du nombre réalisée par le mathématicien Peano à la fin du 19ème siècle.

Dans cet examen de nature épistémologique, Piaget montre comment l'absence explicite d'un recours à l'une ou l'autre des deux dimensions cardinale ou ordinale du nombre entraine la présence implicite de cette même dimension au sein des notions indéfinissable posées dans le système axiomatique proposé par le mathématicien. Au-delà de différences évidentes entre le travail d'axiomatisation réalisé par le mathématicien et les activités par lesquelles la pensée "naturelle" est amenée à construire les opérations logiques et arithmétiques (le premier tendant à exclure de le système axiomatique visé tout ce qui relève de l'activité du sujet, alors que la seconde s'emploie à opérer et à raisonner sans viser la construction d'un tel système), Piaget montre la parenté qui existe malgré tout entre la construction axiomatique et la construction psychogénétique.

D'autres thèmes sont également traité dans ce chapitre, tel que celui de la genèse historique des nombres négatifs, fractionnaires, irrationnels, mais aussi des nombres complexes et des quaternions, ainsi que du transfini (dont certaines propriétés opératoires affaiblissent «leur caractère spécifiquement numérique» et marquent «un retour partiel aux composantes logiques du nombre» (p. 129) en raison de la dissociation qui y est faite entre les ordinaux transfinis et les cardinaux transfinis. Pour chacune de ces catégories de nombres, Piaget montre le rôle fondamental joué, dans leur construction, par l'abstraction à partir des actions et de leurs coordinations, en prenant ainsi le contrepied des conceptions qui accordent un tel rôle à l'abstraction à partir de l'objet. Il montre également comment les difficultés rencontrées dans la construction des nombres négatifs, irrationnels et complexes sont liées au mécanisme de la prise de conscience, qui porte d'abord sur les résultats des actions ou des opérations, avant de porter sur ces dernières. La genèse historique de chacune de ces nouvelles catégories de nombres qui se surajoutent aux "entiers naturels" permet de faire ressortir à chaque fois le rôle prédominant de la pression organisatrice des opérations et des notions numériques préalablement acquises dans la construction, par la pensée mathématique, des nombres négatifs (et du zéro), des irrationnels, des nombres complexes, etc.

Reste alors, trois problèmes épistémologiques majeurs, dont, tout d'abord, celui de la capacité de ces nombres élaborés par abstraction à partir des coordinations d'opérations précédemment acquises à s'appliquer avec succès à la réalité physique au point que les structures qu'ils composent apparaissent comme préadaptées à cette réalité. Puisque les nombres entiers, puis rationnels, puis irrationnels, etc., ne sont pas issus par abstraction à partir des objets et de leur propriété, mais à partir des coordinations des actions puis des opérations logico-mathématiques antérieurement acquises du sujet, la solution que propose Piaget est celle de rechercher dans l'organisation biologique, point de départ des actions du sujet, et elle-même issue de la réalité physique, la raison de cette accord des nombres avec cette réalité. Mais en recourant à un mécanisme d'abstraction portant non pas sur la réalité extérieure mais in fine sur des coordinations d'actions reposant elles-mêmes sur l'organisation vitale, une telle solution ne revient-elle pas, comme la solution empiriste, à rejeter le caractère à la fois fécond et nécessaire des structures numériques? Pour rendre compte de la nécessité, Piaget évoque alors le processus d'équilibration permettant à chaque étape de construction des nombres entiers, puis irrationnels, etc., d'aboutir à des lois de composition réversible et associative des structures garantissant leur nécessité rationnelle. Quant à la fécondité, elle tient au fait que les nouvelles structures ne sont jamais mécaniquement déterminées par les précédentes, le sujet étant appelé, certes en partant de celles-ci d'en créer de nouvelles les dépassant en puissance, en étendue et en stabilité, et ceci par le moyen d'une abstraction et d'une généralisation qui sont à la fois «constructives et réflexives» (p. 141; comme l'équilibration des structures cognitives, ces deux processus d'abstraction et de généralisation portant sur les coordinations les plus générales de l'activité du sujet et non pas, comme dans les épistémologies empiristes, sur les propriétés des objets, feront l'objet d'études spécifiques et d'un examen détaillé lors de la dernière décennie de recherches dirigées par Piaget dans le cadre du CIEG).

En conclusion, ce chapitre permet au lecteur de prendre la pleine mesure de l'approche piagétienne du nombre, et du rôle essentiel qu'elle fait jouer aux actions et opérations du sujet, à leurs coordinations, ainsi qu'aux processus de construction et notamment à cette abstraction réfléchissante (ou "réflexive") et constructrice sur laquelle Piaget reviendra dans la dernière décennie de ses recherches épistémologiques.

Dans ce texte, avant de présenter une position personnelle quant à la question de la foi religieuse, Piaget analyse d'un double point de vue sociologique et psychologique la crise que connaît le protestantisme, alors partagé entre deux attitudes face à Dieu, l'une privilégiant la religion de l'immanence (c'est au sein de la pensée que l'être humain découvre des valeurs universelles qui le dépassent et l'obligent), l'autre la dogmatique de la transcendance, la croyance en un être suprême, et la valeur accordée aux dogmes supposés exprimer la volonté de cet être. Il montre comment ces deux attitudes expriment au moins en partie l'évolution des sociétés et le développement psychologique de l'individu. A la fin des années 1920, et pendant les années 1930, Piaget participe ainsi pleinement aux débats intellectuels de la communauté philosophique romande, en assumant son rôle de savant, mais en le complétant par une réflexion de portée philosophique. On le voit à ce titre reprendre à son compte les thèses du protestantisme libéral, qu'il va réinterpréter à partir de sa propre activité de recherche scientifique et en prenant appui sur la conception philosophique de son ultime maître en philosophie, Léon Brunschvicg (conception qui est une sorte de synthèse en l'idéalisme critique de Kant, qui laissait une place à la croyance en un Dieu transcendant, et l'immanentisme de Spinoza; on admirera en passant, à la page 21 du texte de Piaget, la très fine critique qu'il adresse à la conception morale et religieuse de Kant, où l'on y trouve encore, selon lui, un "résidu d'hétéronomie"…). Dès la fin des années trente et les années 1940, Piaget cessera de participer à des débats qui lui paraîtront vains. Mais toutes les recherches (y compris biologiques) et réflexions qu'il ne cessera d'entreprendre jusqu'au terme de sa vie seront en un sens la continuation de cet effort proposé dans les années 1920 et 1930 de résoudre les questions de fond sur la raison humaine, en prenant toujours appui sur les méthodes scientifiques – les seules à pouvoir, sur le long terme, dépasser les particularismes individuels ou sociaux, et à rendre possible une véritable progression des réponses, pour une partie au moins de ces questions.